Ogni corpo predilige posizioni più basse e più stabili.
Ma è sempre vero?
Prendiamo due rotaie convergenti e dolcemente pendenti che formino un piano inclinato. Su questo rotola, senza sorpresa per nessuno, un cilindro (potrebbe essere un mattarello o un pezzo di tubo) dall'alto verso il basso.
Ora usiamo un altro oggetto, sagomato a doppio cono: questo, lasciato libero di muoversi, va in direzione opposta rispetto al cilindro, infatti si dirige verso quello che lo spettatore ritiene essere "l'alto", lasciandolo letteralmente a "bocca aperta".
Ma.. guardiamolo di profilo e cerchiamo il centro di gravità...

Questo esperimento permette di illustrare un'importante dimostrazione meccanica messa a punto da Galileo a Padova nel primo decennio del Seicento e comunicata in una lettera a Guidobaldo del Monte.
Galileo dimostrò con metodi geometrici che un grave impiega minor tempo a discendere lungo l'arco di una circonferenza che non lungo la corda corrispondente (nonostante che quest'ultima sia più breve).
Galileo, che considerava l'arco come equivalente a un insieme infinito di piani inclinati, non si rese conto che il percorso brachistocrono di un grave che scende tra due punti è l'arco di cicloide, e non l'arco di cerchio.
Il nostro dispositivo si compone di un telaio di legno recante un canale cicloidale e, parallelamente ad esso, un canale rettilineo. Il livello superiore è lo stesso per i due canali come pure il livello inferiore.
Si fanno partire contemporaneamente due biglie lungo i due canali. La biglia che percorre la cicloide arriva in fondo in tempo minore di quella che percorre il piano inclinato.
Perché?

La Cicloide
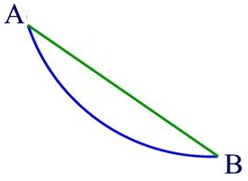
È la curva generata da un punto della circonferenza di un cerchio che rotola su un piano. La cicloide presenta interessanti proprietà fisiche. Infatti, è brachistocrona (il più breve tempo) e tautocrona (lo stesso tempo): brachistocrona perché partendo da un punto A ad un punto B, più basso di A, con velocità iniziale nulla e sotto l’azione della sola forza di gravità, la cicloide è la traiettoria che viene percorsa nel più breve tempo possibile e non l’arco di circonferenza come ipotizzati da Galileo!
La cicloide è anche tautocrona (lo stesso tempo) perché un grave che la percorre senza attrito, per effetto della gravità, giunge nel punto più basso della curva sempre nello stesso tempo da qualunque punto inizi a cadere.
La dimostrazione del brachistocronismo della cicloide fu fornita da Jacques Bernoulli (1654-1705) nel 1697, mentre Christiaan Huygens (1629-1695) ne dimostrò il tautocronismo nel 1659.

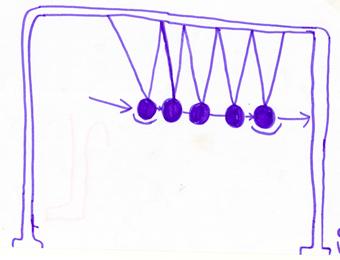Sono delle sfere di acciaio sospese con sottili fili ad un solido supporto metallico.
Quando sono ferme tutte le sfere sono a contatto una con l'altra.
Spostando una biglia e lasciandola cadere vedremo, quando questa colpisce la fila ferma, che soltanto la biglia all'estremità opposta subisce un rimbalzo allontanandosi velocemente, mentre quelle centrali restano praticamente immobili.
Ripetiamo la prova spostando due biglie: rimbalzeranno le due biglie opposte!

Le biglie di Newton si spiegano con due leggi fisiche fondamentali: il principio di conservazione della quantità di moto e quello di conservazione dell'energia.

Due contenitori cilindrici praticamente identici, di ugual peso, pieni di pallini di piombo, oscillano su due guide sagomate ad arco.
Facendo partire dall'alto e contemporaneamente i due cilindri, ci accorgiamo che uno dei due si arresta decisamente prima dell'altro.
Cosa è successo:
Nel cilindro oscilla sulla guida più a lungo i pallini sono strettamente serrati per mezzo di due dischi di plastica, in modo che non si possano muovere e che formino una massa unica con il contenitore che quindi il perde energia solo per l'attrito con la rotaia e con l'aria.
Nel secondo cilindro invece i pallini hanno un spazio maggiore e sono liberi di muoversi all'interno del contenitore. durante il moto perdono energia disordinatamente in attriti interni a scapito del moto di insieme, quindi il cilindro si arresta rapidamente nel punto più basso della guida.

Le ruote di bicicletta sono maneggevoli se ferme, mentre se ruotano non sembrano altrettanto docili, infatti oppongono resistenza ad ogni tentativo di cambiare la direzione dell'asse di rotazione.
Alcuni "giochi" per scoprire la conservazione del "momento angolare " del moto degli oggetti, capire perché in bicicletta non si cade e come funziona un giroscopio, strumento necessario per mantenere l'assetto nelle navi e negli aerei.

Due semisfere di plastica sono appoggiate una sull'altra a formare una "bolla".
Con un fornelletto ad alcool facciamo "bruciare" un po' dell'aria dentro la bolla.
Ci accorgeremo leggendo il barometro che la pressione interna diminuisce, di poco, ma quanto basta per rendere difficilissimo staccare le due semisfere con le mani.
Incredibile! L'aria che ci circonda ha una forza enorme!

Otto von Guericke discendente di una agiata famiglia di Magdeburgo, studiò legge alle università di Lipsia (1617-1620), Helmstedt (1620) e Jena (1621-1622), poi frequentò corsi di matematica e cominciò ad occuparsi di problemi ingegneristici. Negli anni tra il 1646 e il 1676, tenne la carica di borgomastro di Magdeburgo e nonostante il suo tempo fosse largamente assorbito dalla vita pubblica, von Guericke continuò ad occuparsi di scienza sperimentale e ideò e realizzò - pur tra molti insuccessi - tanti esperimenti barometrici per capire a fondo il problema della pressione dell'aria.


È nell'ambito di questi interessi che, nel 1657, von Guericke realizzò il suo più famoso esperimento
Due semisfere di bronzo di circa 50 cm. di diametro perfettamente combacianti vennero unite l'una all'altra e al loro interno fu prodotto il vuoto mediante una pompa pneumatica.
Incredibilmente, per separare le due componenti occorreva la forza congiunta di due pariglie di 8 cavalli, che tiravano in direzioni contrapposte.

Confermò così tutte le scoperte torricelliane ed evidenziò i sorprendenti effetti della pressione atmosferica.
La versione qui esposta è costituita da due emisferi trasparenti di 40 cm di diametro, contenenti un barometro ed un piccolo fornellino ad alcool.
La fiamma del fornellino brucia, fino a spegnersi, parte dell'aria è racchiusa nella sfera (l'alcool reagisce con l'ossigeno), e riduce di circa il 10% le moli di gas contenute inizialmente nella sfera. La pressione interna cala della stessa percentuale e non riesce più a bilanciare la pressione atmosferica che comprime le due semisfere l'una contro l'altra con una forza pari alla forza peso di una massa di 120 Kg!
Questo valore si può ricavare facilmente sapendo che la pressione atmosferica produce una forza di circa un Kg peso per cm2 e che la pressione interna è ridotta a 900 g/cm2.
Il differenziale interno-esterno di 100 g/cm2 applicato su la superficie di una circonferenza massima della sfera (1200 cm2) dà appunto approssimativamente il valore sopra indicato.

Questa esperienza è un esempio classico del trasferimento dell'energia.
I due pendoli sono solidali con lo stesso supporto e possono venire collegati in varie maniere, generalmente si fa con fili elastici, con molle ma si può sfruttare semplicemente anche l'elasticità del supporto stesso. facendo partire un pendolo, vedremo pian piano smorzarsi il suo moto, a favore del secondo pendolo che inizierà a muoversi, fino a raggiungere l'ampiezza massima, quando il primo pendolo sarà fermo. Ma subito il processo si inverte e il secondo pendolo rallenta, mentre il primo riparte...
Si potrà verificare che, se l'accoppiatore è poco efficace, l'alternanza dei due moti avviene con ritmo lento, ossia con periodo lungo.
Ed ecco la spiegazione fisica del fenomeno: il pendolo che viene azionato tende a trascinare con sè quello fermo tramite il moto del filo orizzontale (o dell'accoppiatore) ; quest'ultimo, partendo con un certo ritardo, ha l'effetto di agire da freno sul primo, rallentandolo. L'effetto va crescendo nel tempo finché i ruoli si scambiano.

Sembra una trottola come tante, ma quando la facciamo ruotare abbiamo la sorpresa di vederla capovolgere su se stessa per continuare poi a ruotare sul picciolo, cioè la punta che avevamo preso fra le dita per darle la spinta.
Non e' un trucco, ma il risultato di alcune leggi fisiche che operano durante il moto di questo oggetto!

Fa parte della categoria delle trottole speciali. Fu scoperto da alcuni archeologi e fu chiamato anche pietra celtica.
Ha un verso di rotazione preferenziale:
se fatto ruotare dalla parte "giusta", si mantiene il moto normalmente, se invece si fa ruotare "controsenso", dopo poco l'oggetto comincia ad oscillare sempre più stranamente e poi, si ferma quasi e riparte nell'altro senso.
Il suo comportamento è dovuto ad una non-simmetria nella forma, che si può ottenere anche con una non simmetria nella distribuzione dei pesi.

Lo lanci allontanandolo dal suo centro di riposo ed esso inizia ad oscillare come un qualsiasi pendolo, ma attenzione.....non va dritto come ti aspetti!
Il pendolo non oscilla sempre sullo stesso piano, ma devia come spinto da una forza misteriosa e descrive cerchi, poi ellissi e quindi ritorna su di un nuovo piano; ma non è finita.... esso riprende a girare e a compiere traiettorie curve in senso opposto a prima!
Sembra proprio che questo pendolo si muova in modo assurdo...
Il fenomeno, come ti illustreranno sul posto, dipende dal tipo di attacco fra il filo del pendolo e il supporto che obbliga il pendolo a muoversi lungo una "inaspettata quanto strana" traiettoria.
Il moto, come scoprirai, è la sovrapposizione di due possibili oscillazioni diverse in frequenza, e quasi, quasi potresti immaginarti di vedere lì non un pendolo, ma due accoppiati...
Esistono due direzioni di oscillazione secondo le quali il pendolo si comporta come un pendolo singolo, questi rappresentano anche i piani di simmetria dei "piani preferenziali di oscillazione" durante il moto caotico.
Questo tipo moto è in realtà solo apparentemente caotico in quanto può essere ricostruito matematicamente unendo le equazioni del moto dei due pendoli che lo compongono.